The Primary School Leaving Examination (PSLE) is a crucial milestone for Singaporean students, and mathematics is one of the most challenging subjects. In 2023, the PSLE math paper featured some particularly tricky questions. Let’s explore the 5 most difficult questions from the 2023 PSLE math paper and break down the solutions step-by-step, helping students tackle these challenges effectively.
Question 1: Dividing Teams Equally
(Adapted from PSLE 2023, Paper 1, Question 14)
Problem:
Mrs. Wong wanted to divide 72 girls and 60 boys equally into as many teams as possible. Each team had the same number of children. The number of boys in each team was the same. How many boys were there in each team?
Solution:
To solve this problem, we need to find the maximum number of teams that can be formed with an equal number of boys and girls in each team.
- Identify the common factors of 72 and 60.
The greatest common divisor (GCD) of 72 and 60 is 12. Thus, the number of boys per team can only be a factor of 12. - Check each factor:
- 2 boys per team: 60 ÷ 2 = 30 teams. However, 72 girls cannot be divided into 30 equal teams.
- 5 boys per team: 60 ÷ 5 = 12 teams. This works because 72 girls ÷ 12 teams = 6 girls per team.
Thus, the answer is 5 boys per team.
Question 2: Calculating Liquid Volumes
(Adapted from PSLE 2023, Paper 1, Question 29)
Problem:
Gopal had 3 identical tins of paint filled to the top. He poured 760 ml out of each tin. The total amount of paint left in the 3 tins after pouring was equal to the amount of paint in 1 tin at first. What was the amount of paint in each tin at first?
Solution:
To find the amount of paint initially in each tin, we need to understand that the total paint left equals the initial amount in one tin.
- Calculate the total amount poured out:
760 ml × 3 tins = 2280 ml - Determine the remaining paint:
Since the remaining paint equals the initial amount in one tin, the total paint left is half the initial amount. - Find the initial amount in each tin:
Initial amount = 2280 ml ÷ 2 = 1140 ml
Thus, each tin initially contained 1140 ml of paint.
Question 3: Fraction Calculation
(Adapted from PSLE 2023, Paper 2, Question 5)
Problem:
A problem involving ratios where the numerator and denominator must be adjusted to maintain a consistent ratio across different scenarios.
Solution:
To solve fraction problems like this, students need to be careful with ratios, especially when adjusting for changes in the numerator or denominator. A common mistake is only adjusting the numerator.
- Ensure ratio consistency:
If a bag contains twice as many pens, both the numerator and denominator must be adjusted equally to maintain the ratio. - Apply the change:
Multiply the ratio by the necessary factor to ensure the values align correctly.
By methodically adjusting both parts of the fraction, the correct solution can be found.
Question 4: Grid Formation Analysis
(Adapted from PSLE 2023, Paper 2, Question 11)
Problem:
Jean used rods and straws to form grids. Initially, she made a grid that was 2 rods long and 3 straws wide. She then made a larger grid that was 3 rods long and 4 straws wide. How many rods and straws were there in this grid?
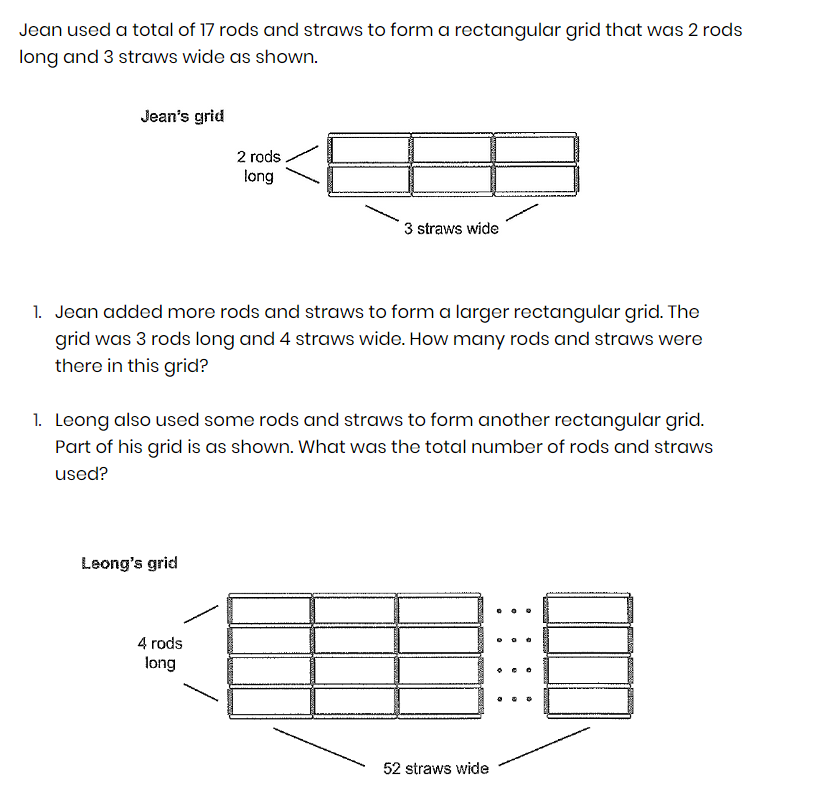
Solution:
- Identify the pattern:
- For rods: Multiply the number of rods by (strands + 1).
- For straws: Multiply the number of straws by (rods + 1).
- Calculate for the larger grid:
- Straws: 4 × (3 + 1) = 16
- Rods: 3 × (4 + 1) = 15
Thus, the grid consists of 16 straws and 15 rods.
Question 5: Perimeter and Area Calculation
(Adapted from PSLE 2023, Paper 2, Question 17)
Problem:
Figure 1 is a trapezium with a perimeter of 96 cm. Jiayu joins three such trapeziums to form Figure 2, with a perimeter of 204 cm.
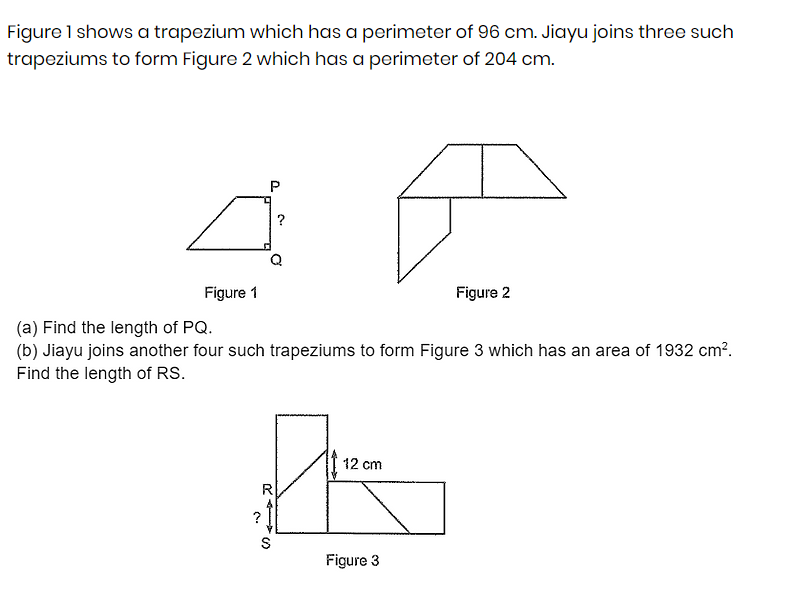
Solution:
To find the length of PQ, the line that overlaps when the trapeziums are joined:
- Calculate the total perimeter without overlap:
3 × 96 cm = 288 cm - Subtract the given perimeter of the new figure:
288 cm – 204 cm = 84 cm - Determine the length of each PQ segment:
84 cm ÷ 4 (overlaps) = 21 cm
Thus, each PQ segment measures 21 cm.
Why Choose Daniel’s Math Tuition?
At Daniel’s Math Tuition, we specialize in preparing students for PSLE math with a focus on understanding and applying core concepts. Our unique approach ensures students grasp the fundamental principles, enabling them to tackle even the most challenging questions with confidence. Our lessons are aligned with the latest MOE syllabus, and we offer a variety of resources to support students outside the classroom. Our comprehensive after-class materials include recorded lessons, detailed revision papers, and explanatory videos, ensuring that students have all the tools they need to succeed.
Enroll your child in Daniel’s Math Tuition today and watch them excel in Primary Maths!
