After working hard on Primary School Math for 6 years, the PSLE Math paper is the final hurdle in your child’s Mathematics journey. However, it often ends up being extremely challenging thanks to trick questions and complicated concepts. The Math paper is notorious for being difficult, and countless students have fallen for these traps.
At Daniel Math Tuition, we’ve seen firsthand how tricky PSLE Math questions can really throw students off—not because the content is unfamiliar, but because the way the question is asked forces them to think differently.
In this article, we’ve picked 5 past-year PSLE questions that caused a stir—and more importantly, explain why they were so tough and how your child can learn to tackle questions like these. While these questions will most likely not reappear, learning the required approach will help your child avoid similar traps in the future.
1: Triangle Patterns (2019)
This 2019 question tested students on pattern recognition. What makes this question tough is the jump to Figure 250. As it is a massive leap, students are left unable to guess, and have to correctly determine the pattern, establish the rule, and then apply it to the diagram. This question is a test of whether they really understand how to work with sequences and generalise.
Solution:
Students should begin by listing down all the information they have access to. For example, here are some facts that they can make use of:
- Even-numbered figures have more grey triangles than white triangles.
- Odd-numbered figures have more white triangles than grey triangles.
- The total amount of triangles in each figure is the square of each figure.
- Only one colour of triangle increases with each successive figure.
From here, they can begin solving part (a). Figure 5 will have 25 triangles in total, as per the third rule they have determined.
As per the second rule, figure 5 will have more white triangles, as the amount of white triangles has just increased. Thus, as the 10 grey triangles remain the same, there must be 15 white triangles.
Moving on, students need to use the third rule again, in order to solve part (b). Making this connection helps to simplify the question significantly. They just need to multiply 250 by itself, to find the answer
250 x 250 = 62500
Thus, there are 62500 triangles in figure 250.
Finally, in order to find the percentage in part (c), they need to identify one last relationship between the triangles. By making this connection, they can avoid being stumped by the question.
- The difference between grey and white triangles is equal to the figure number.
With this, they are able to determine that there are 250 more grey triangles than white triangles in figure 250, as it is an even number.
Grey triangles + White triangles = 62500
(62500-250)/2= 31125 (White Triangles)
31125+250 = 31375 (Grey Triangles)
31375/62500 x 100 = 50.2
Through this method, the student is able to determine that 50.2% of the triangles are grey. The key to this question was not the calculation, but the student’s information gathering skill and deductive ability. Identifying these five key rules can help them solve it, without needing to use brute force to estimate what figure 250 would be, or to simply guess. This type of pattern recognition is a highly valuable tool for a student.
2: Printing Machines (2013)
Questions about speed and rate are one of the most common trick questions for students. If a student has not encountered them before, they may try to solve it purely on mathematical terms, without considering that time cannot always be smoothly divided.
Solution:
For part (a), the student simply needs to subtract 100 minutes from 1pm. This equals to 1 hour and 40 minutes, making it 11:20 am when it first began.
For part (b), the trick was to determine the amount of papers printed by using the difference in time.
- The Faster Machine completed its job in 70 minutes.
- The Faster Machine prints 6 more copies a minute than the Slower one.
- By the 70 minute mark, it has printed 420 MORE copies than the Slower Machine.
- In the next 30 minutes, the slower machine must print at a constant rate of 420/30 copies per minute in order to complete its job.
- 420/30= 14 copies per minute.
- Over the 100 minutes, the slower machine printed 14×100= 1400 copies.
- As both machines printed the same amount of copies regardless of rate, the total amount is simply:
1400×2= 2800 copies.
Students needed to understand the relationship between speed, time, and quantity, and then apply mathematical reasoning to solve the problem. The multi-step nature made it difficult for many students.
3: Semicircles (2019)
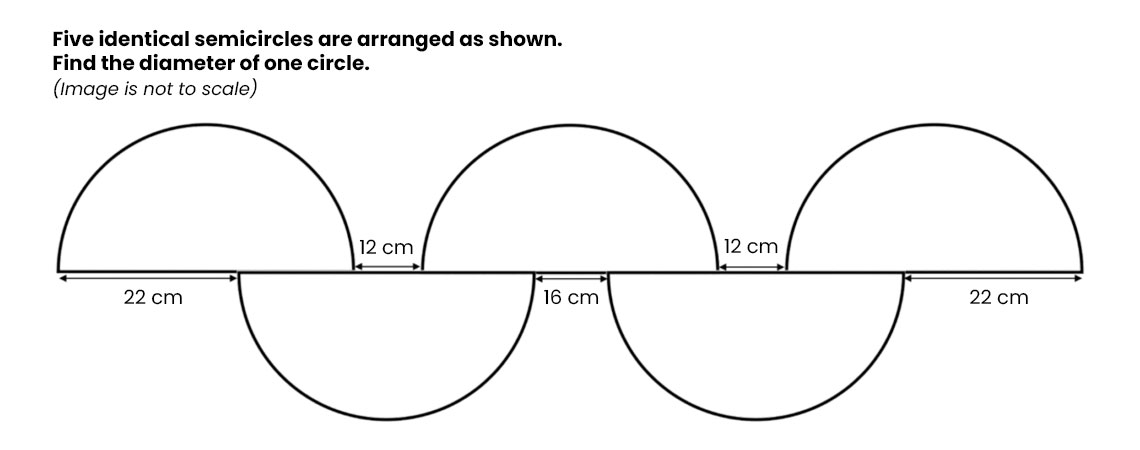
This question revolves around geometry, requiring students to find out the diameter of a circle using incomplete information. Many students found this exceptionally difficult, as they were confused by the large variation in figures given across the five semicircles.
Solution:
This question was challenging for students because they were left unable to cleanly divide the slightly different distances between the semi circles, yet were tasked with finding out the full diameter of a circle.
The best way to solve this question is to recognise that there is a common length in the middle of the semicircles that overlap. Hence, the back of the semicircle, excluding the overlapping length is 22cm. Students can subtract 22cm – 12cm To get 10cm.
As both sides are 10cm, students can add 10cm + 10cm + 16cm, to get 36cm in diameter.
4: Coin Weight (2021)
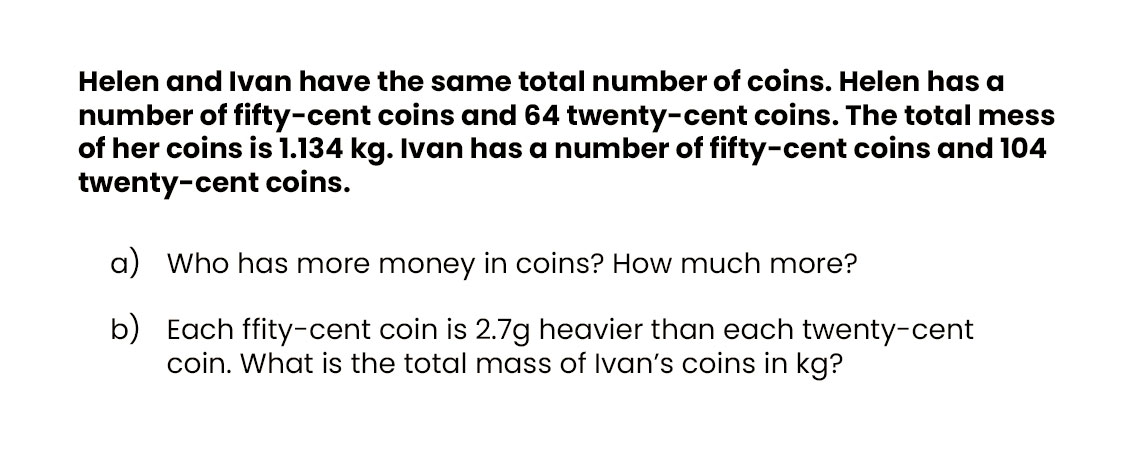
This 2021 question combines money calculations with logical reasoning and unit conversion. Many students struggled because they focused too much on trying to calculate the total number of coins.
Solution:
Most kids get stuck thinking they need to know how many coins there are. However, it is impossible to determine the total amount of money each person has using the information given, making the actual number irrelevant. The key is realising that both Helen and Ivan have the same total number of coins, just different types. Once that clicks, it’s all about comparing the differences. This kind of logic-based thinking is what they’re looking for in the exam.
In part (a), students are asked who has more money in coins, and by how much.
Helen has 64 20-cent coins. Ivan has 104. Since they both have the same total number of coins, Helen must have more 50-cent coins to make up for having fewer 20-cent coins. Specifically, she has 40 more 50-cent coins than Ivan. Therefore, Ivan must have 40 more 20-cent coins than Helen.
This difference is what the question is testing. Rather than trying to determine how many coins they each have in total (which is not possible from the information given), students should realise the values cancel out, and only the extra 40 coins on either side matter.
- Helen’s 40 extra 50-cent coins = 40 × $0.50 = $20
- Ivan’s 40 extra 20-cent coins = 40 × $0.20 = $8
- Difference = $20 – $8 = $12
So, Helen has $12 more than Ivan.
For part (b), students needed to use logical substitution. The key point is that they do not need to know the exact numbers of coins in order to begin work.
- A 20-cent coin weighs a certain amount.
- A 50-cent coin weighs 2.7 grams more than the 20-cent coin.
So since each 20-cent coin is 2.7 grams lighter, students can figure out that 40 20-cent coins weigh 108 grams less than the 50-cent coins.
1134-108=1026
Meaning that Ivan’s coins weigh 1.026kg.
5: Ribbon Length (2017)
Our last question here is a bit simpler, but still has potential to trip up students, and serves as an example of how careful thinking is more important than blindly following formula. Students who got this question wrong were so focused on basic division that they didn’t think practically and account for real-world constraints. An INCORRECT method might be:
200 Ribbons x 100cm = 22000cm of Ribbon needed.
22000/2500cm(25m) = 8.8 rolls.
However, this is wrong, as it does not account for the fact that each roll of ribbon is its own length, and multiple sets cannot be added together.
Solution:
Each ribbon must be 110 cm long. Jess needs 200 ribbons.
200 × 110 = 22,000 cm of ribbon needed in total.
Each tape is 25 m long, which is 2500 cm.
However, a single tape can only be cut into full ribbons.
2500/110= 22.72.
Contrary to what students might have learnt about rounding up and down, they are not able to physically round up this number when they are dealing with a real-life ribbon. Therefore, they can only take it as 22 ribbons per roll of tape.
To get 200 ribbons, they will need to divide it by 22, to get 9.09. This number, as they’ve learnt, cannot be rounded down. Therefore, Jess needs 10 ribbons.
Help Your Child Tackle Difficult PSLE Math Questions with Confidence
These aren’t just “hard” questions — they’re designed to see how well a student can think on their feet. Students need logical reasoning, pattern recognition, and the ability to adapt to new problem types. That’s why at Daniel Math Tuition, we focus not just on drilling content, but helping students spot patterns, avoid common traps, and approach unfamiliar problems with confidence. We also cover multiple types of word problems, in order to prepare students for these trick questions and improve their problem solving skills.
Daniels Math Tuition offer a PSLE Bootcamp during the June/September holiday period, to help finalise your child’s PSLE preparation! This 3-day long, 12 hour Math Bootcamp allows students to review key concepts, experience exam-style questions, and master problem-solving. We place emphasis on strong understanding of math fundamentals, and this targeting approach equips students to perform their best in stressful situations. Find out more by contacting us today.
We also hold regular weekly lessons, that are designed to sharpen your child’s thinking and boost their exam readiness with a structured approach to Primary 6 Math. If you’d like your child to train this kind of thinking, you can learn more about our Primary 6 Math Tuition classes here.
